Korak 1. Znakovi u poruci poredani po učestalosti
Zavod za elektroničke sustave i obradu informacija
Fakultet elektrotehnike i računarstva
Sveučilište u Zagrebu
Vizualizacija Huffmanovog algoritma za komprimiranje podataka
Seminarski rad iz PVPRM-a
1. Uvod u tehnike komprimiranja
2. Huffmanov algoritam kompresije
3. Varijacije na temu Huffmanov algoritam
4. Primjene Huffmanovog algoritma
5. Linkovi na demonstracijske stranice
1. Uvod u tehnike komprimiranja
Kao uvod u područje komprimiranja podataka možemo spomenuti da postoje dva
glavna oblika sažimanja ili komprimiranja podataka. Komprimiranje s gubicima
(engl. lossy) ili komprimiranje bez gubitaka (engl. lossless).
Komprimiranje s gubicima nije loše samo zato što dolazi do gubitaka. Dapače,
u nekim situacijama gdje ljudska osjetila ne percipiraju potpunu informaciju,
poželjno je da se neki bitovi kao mali djelići informacije odbace kako bi se
sadržaj što više komprimirao a da nije izgubio na kvaliteti. Takav primjeri
su razni algoritmi za komprimiranje slika ili zvuka.
Komprimiranje bez gubitaka nastoji sažeti bitovnu duljinu podatka što je više
moguće a da pritom ne dođe do ikakvog gubitka informacije. Ovakve metode se
koriste kad je potreban apsolutno svaki bit za informaciju, u situacijama gdje
promjena makar jednog bita dovodi do potpune promjene informacije.
Huffmanov algoritam kompresije
1951. godine David Huffman je kao student imao zadatak pronaći najefikasniji
algoritam komprimiranja. Taj zadatak mu je zadao njegov profesor Robert M. Fano.
Nakon isprobavanja postojećih algoritama, Huffman je došao do ideje i izmislio
algoritam koji je bolji od algoritma njegovog profesora. Algoritmi su doduše
bili slični, ali je Huffmanov pokazivao veću efikasnost u komprimiranju.
To je ujedno bilo i prvo rješenje koje je odgovaralo komprimiranju s minimalnom
redundancijom kojom se postiže najbolji omjer komprimiranja. To vrijedi naravno
za komprimiranje u određenim situacijama jer je za neke druge primjene bolji
neki drugi algoritam.
Osnovna ideja kod Huffmanovog algoritma je dodijeliti najkraće kodne riječi
onim blokovima koji imaju najveću vrijednost ponavljanja i obrnuto. Sličan pristup
koristi i Morseov kod.
No rečena ideja se može realizirati na razne načine. Promotrimo sljedeće tablice:
| Simbol | A | B | C | D |
| Kodna riječ | 0 | 1 | 10 | 11 |
Tablica 1.
Na tablici 1. je jedna od realizacija ideje dodjeljivanja kodnih riječi. Međutim ovakav način nema nikakvu praktičnu svrhu. Npr. neka prijemnim kanalom dođe poruka: 0110. Ona može biti interpretirana kao ABBA, ADA ili ABC.
| Simbol | A | B | C | D |
| Kodna riječ | 0 | 10 | 110 | 111 |
Tablica 2.
U ovom slučaju će primljena poruka 010111000 biti pravilno dekodirana kao ABDAAA.
Grafičkim prikazom Huffman kodiranja se može dobiti bolji uvid u stvar. Prije postupka kodiranja, kao ulaz u algoritam dovodi se znak ili skup znakova koji se treba kodirati. Zajedno sa svakom jedinkom dolazi njena vjerojatnost pojavljivanja. Algoritam glasi:
Promotrimo kako algoritam funkcionira na primjeru poruke: OVO JE MOJ SEMINAR!!!!
SIMBOL |
BROJ POJAVLJIVANJA |
VJEROJATNOST POJAVLJIVANJA(%) |
O |
3 |
13.63 |
V |
1 |
4.55 |
M |
2 |
9.09 |
E |
2 |
9.09 |
J |
2 |
9.09 |
S |
1 |
4.55 |
I |
1 |
4.55 |
N |
1 |
4.55 |
A |
1 |
4.55 |
R |
1 |
4.55 |
space |
2 |
13.63 |
! |
4 |
18.18 |
UKUPNO |
22 |
100 |
Tablica 3.
U u prvom stupcu gornje tablice nalaze se svi znakovi koji su u poruci, u drugom stupcu je broj pojavljivanja tih znakova, a u trecem njihova relativna frekvencija pojavljivanja.
1. Poredamo simbole prema opadajućim vjerojatnostima, tj. broju pojavljivanja
! |
4 |
space |
3 |
O |
3 |
M |
2 |
E |
2 |
J |
2 |
V |
1 |
S |
1 |
I |
1 |
N |
1 |
A |
1 |
R |
1 |
Tablica 4.
Korak 1. Znakovi u poruci poredani po učestalosti
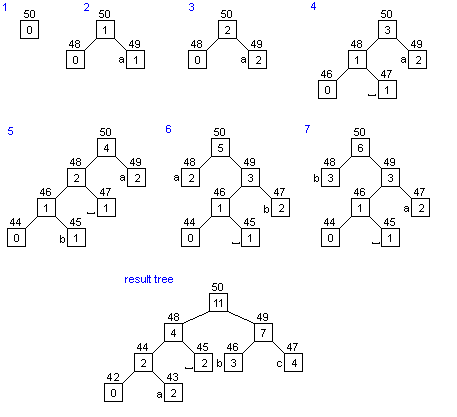
2. Udružujemo simbole zbrajajući njihove brojeve pojavljivanja, počevši od najmanjih
Korak 2.
Korak 3.
Korak 4.
Korak 5.
Korak 6.
Korak 7.
Korak 8.
3. Desnim granama pridružujemo 1, a lijevima 0
Korak 9.
4. Krenuvši od vrha stabla čitamo redom 0 i 1 koji vode do pojedinog simbola. Na slici je prikazan primjer za čitanje koda simbola V, te simbola !
Korak 10.
Simbol V prikazan Huffmanovim načinom kodiranja je 1111, a simbol ! se prikazuje kao 010. Ostali simboli prikazani su u tablici.
! |
010 |
space |
000 |
O |
001 |
M |
100 |
E |
0111 |
J |
0110 |
V |
1111 |
S |
1110 |
I |
1101 |
N |
1100 |
A |
1011 |
R |
1010 |
Tablica 5.
Vidljivo je da simboli sa većom vjerojatnošću pojavljivanja imaju kraći zapis.
U praksi se Huffmanov algoritam koristi tako da se zajedno s komprimiranom
datotekom na početku slanja pošalje i stablo iz kojeg se očitaju kodne riječi.
Ovo može ponekad uzrokovati probleme. Što ako se radi o nekom live update-u?
Doći će do promjene učestalosti nekih ili svih znakova. Rješenje problema leži
u adaptivnom Huffmanovom algoritmu.
Adaptivni algoritam je jednostavan:
Inicijaliziraj stablo
Za svaki novi znak {
Kodiraj znak
Osvježi stablo
}
Kraj
Dekodiranje radi na isti način. Sve dok i odašiljačka i prijemna strana imaju
isti početni model stabla i osvježeni model stabla, obje strane će imati iste
informacije.
Međutim, problem je sad u osvježavanju stabla (ili modela stabla). Najjednostavnije
je krenuti svaki put ispočetka kad se pošalje novi znak. Ovakvim načinom osvježavanja
bi dobili jako spor algoritam. Trik je u tome da se osvježavaju samo djelovi
stabla na koje je dolazak novog znaka utjecao.
Varijacije na temu Huffmanov algoritam
i drugi...
Primjene Huffmanovog algoritma
Primjenjuje se kod komprimiranja teksta i programskih datoteka (zbog svojstava navedenih u uvodu). Konkretno Huffmanov algoritam možemo pronaći u poznatim programima kao što su: pkZIP, gz, arj i drugi. Također se koristi unutar JPEG, MPEG i MP3 algoritma.
Linkovi na demonstracijske stranice:
Linkovi na izvještaj i prezentaciju:
Ovaj rad je rezultat truda trojke iz tima Flairoviti, a oni su: