Fraktalna Kompresija Slika
1. Uvod
Prošlo je već 20 godina otkada su fraktana tehnika predstavljena u računalnoj grafici. Te ideje zasnovane su na matematičkoj teoriji nazvanoj IFS (Itreated Function Systems) koju je predstavio i razvio australski matematičar John Hutchinson 1981 godine. Ubrzo zatim Michael Barnsley, proširuje teoriju IFS uvođenjem Collage teorema koji govori koje uvijete treba zadovoljiti IFS ukoliko se njome žele generirati slike. To dakako otvara intrigantne mogućnosti. Ako je fraktalna matematika dobra za generiranje slika prirodnih oblika (drveća, oblaka, listova, planina,…), da li je njome moguće komprimirenje slika? Polazeći od neke date slike koristeći IFS tako da se generira orginalna slika(manje ili više točno), poznati je problem inverzije (problem kodiranja slike ) .1988 taj problem rješava tada vodeći student Barnsley-a , Arnaud Jacquin uvodeći modificiranu verziju IFS tz.Partitionet Itreated Function Systems (PFIS).Ideja Jacquina je vrlo jednostavna. Sliku koju želimo kodirati ne smijemo promatrati kao kolaž kopija cijele slike, već kao kolaž kopija manjih dijelova slike. Npr. zamislimo sliku planine i oblake nad njome, dio oblaka ne izgleda slično cijelom krajoliku kojeg čini planina , oblaci i nebo, već tu sličnost vjerojatno moramo pronaći nekom drugom oblaku ili u nekom drugom dijelu slike. Dakle cijela zamisao leži na traženju sebi-slični dijelova na slici …
2. Što je to Fraktalna Kompresija Slika
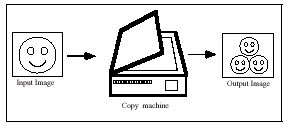
Zamislimo da imamo poseban fotokopirni stroj koji ulaznu sliku kopira tako da je dvostruko umanji i umnoži tri puta , kao što je to prikazano na slici 2.1

slika 2.1.Način kopiranja ulazne slike .
Što će se dogoditi ako izlazu sliku vratimo na ulaz fotokopirnog stroja, a da način kopiranja ostane isti? Slika 2.2. pokazuje nekoliko iteracija tog procesa sa nekoliko različitih početnih slika.
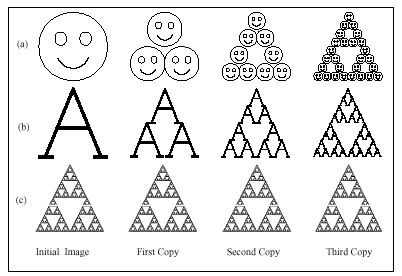
Slika 2.2. Prve tri kopije generirane kopirkom iz slike 2.1.
Što možemo primijetiti? Sve kopije konvergiraju prema istoj konačnoj slici(image-u),
prema image-u iz slike 2.2.c tz. Sierpinski trokut. Ta konačna slika naziva se atrractor za taj fotokopirni stroj. Također se može primijetiti da ta konačna slika – attractor nije promijenjena procesom ,jer otkad je formirana od tri reducirane kopije od sebe same, ona ima taj detalj u svakom stupnju – to je fraktal. Fotokopirna mašina proizvodi slike sebi-slične nazvane fraktali.Općenito kažemo da je neki skup F fraktal ako ima slijedeća svojstva:
Vratimo se fotokopirnoj mašini uz primjedbu,sve dok krajni rezultat fotokopirne mašine koja radi u povratnoj vezi određen na način kako se transformira ulazna slika u kopiju, potrebno je samo opisati te transformacije da bismo dobili odgovarajući attractor. Različite transformacije vode do različitih attractora , sa tehničkim ograničenjem da transformacije moraju biti kontraktivne – a to je, da dane transformacije pridružene bilo kojim dvjema točkama u ulaznoj slici moraju dovesti bliže te točke na kopiji. Osim tog tehničkog ograničenja,možemo odabrati transformacije bilo kojeg oblika. U praksi, odabirom transformacija oblika
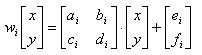
dovoljno je da izgeneriramo veliki i zanimljivi set attractora. Takve transformacije zovemo afine transformacije ravnine, i svaka može rastezati, skalitati, kositi(naheriti), rotirati i translatirati ulaznu sliku (image)
M. Barnsley je uvidio da spremanjem slika kao kolekcije transformacija može voditi ka kompresiji slika. Njegovi argumenti leže u mogučnosti da se slika opiše sa nekoliko parametara afinih transformacija. Ako imamo parametre afinih transformacija(ili fotokopirne mašine) tada možemo generirati sliku.

Slika 2.3. Slika Barnsleyjeve parati koja se može generirati iz samo četri afine transformacije (svaka trensformacija sadrži šest parametara)
Svaka afina transforacija wi je definirana sa šest parametara, ai , bi , ci , di , ei i fi koja ne zahtijeva puno memorije za pohranu . Paprat može biti pohranjena sa 4 transformacija * 6 parametara za transformaciju * 32 bita za parametar = 768 bitova, dok pohranjivanje paprati kao kolekcije piksela, zahtijeva mogo više memorije( najmanje 65,536 bitiva za rezoluciju prikazanom slikom 2.3 ). Kompresijski omjer (ratio) iznosi 65,536/768= 85. 33
što je vrlo visoki omjer.
Ali kako pronaći potrebne parametre za bilo koju danu sliku i na taj način je kompresirali? (već ranije spomenuti problem inverzije). Barnsley-jev san je bio ponaći algoritam za računanje tih parametara. Međutim, slike koje nalazimo u prirodi uglavno su vrlo neprikladne za generiranje koristeći afine transformacije, a tome je tako jer slike iz prirode nisu upravo sebi-slične(self-similar ) tj. nisu fraktalne strukture. Tako Barnsley-jev san se nije ostvario. Međutim, postoje trikovi kojima je moguće riješiti problem inverzije. Pitanje je samo koliko su oni dobri u kodiranju slika. No prije svega treba objasniti Iterated Function Systems zato što je Fraktalna Kompresija slika igrađena na njoj.
3. Iterated Function Systems (IFS)
Ponašanje fotokopirne mašine možemo opisati pomoću matamatičkog modela Iterated Function systems (IFS). Iterirani sistem funkcija sastoji se od kolekcije kontraktivnih afinih transformacija. Ta kolekcija transformacija definira mapu W
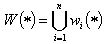
Mapa W nije pridružena ravnini, već je pridružena skupovima – a to su zbirevi točka u ravnini. Za neki ulazni skup (ili sliku) f, možemo izračunati wi za svaki i (to odgovara stvaranju reduciranih kopija od ulazne slike f ), uzmemo uniju tih skupova(to odgovara načinu na koji se sklope reducirane kopije) i dobijemo novi skup W(f)(izlazna kopija ). Nazovimo podskupove ravnine imgesima(imiđima). Hutchinson je dokazao vrlo važno svojstvo IFS-a: ako je wi kontraktivna u ravnini, tada je W kontraktivna na prostoru(zatvorenih i ograničenih) podskupova ravnine. Hutchinson-nov teorem na govori, da ako imamo kotrahirajuću mapu na prostoru image-a , tada postoji poseban image tz . attractor označen sa xW , sa slijedećim svojstvima:
W(xW)= xW = w1 (xW ) U w2(xW ) U , . . . U wn(xW ) 3.1
xW = foo = limn-> oo Won(f0)
koji ne ovisi o izboru f0
U nešto rigidnijoj formi, ta tri pravila poznata su kao Contrative Mapping Fixed Point Theorem.
4. Self – Similarity kod Slika
Sada želimo pronaći mapu W